PL教程 第一章 人和机器

首先我得说，本来这些杂七杂八要放在前言里讲的，结果是… 想说的话实在太多，前言已经尽可能地收敛了，还是不知不觉扯远了，前言越到后面写的越跟编程没关系了。所以现在简单说说吧。

又要提 Dijkstra 的名言了(我怕不是要变成 Dijkstra 的粉丝了…)

教一群被 BASIC 语言先入为主的学生，什么是好的编程风格，简直是一件不可能的事。对于一些有潜力的程序员，他们受到的智力伤害远远超过了重建他们的信心。

(哈哈，我们学校教的就是 Basic)

语言就是人表达的方式，语言塑造了信息的世界。

受应试教育的影响，很多人接触编程就是从算法竞赛开始的，然后被老师灌输过他们的理论以后，理所当然地认为编程就是算法、数学。当然，很多人跟不上进度便不学了，跟我一样，这是好事。

我现在也不知道这些误解到底是从哪来的，但我发现编程跟写作真的很像，算法就是那些写作手法，数学可以比作一些特定的知识，比如历史。你可以教小学生再多的手法和各种知识，但不要指望有人能写出好的故事。

原因在于，写作唯一的目的是表达自己的想法，编程就是为了解决问题。要写一篇好文章，一些手法必不可少，但是重要的东西还有很多，学习手法也要建立在文章写的清楚的基础上。另外，如果要写三国演义，那必须精通历史，但也有很多时候用不着那么高深的历史。
编程就是一样的道理。

所以我想按程序语言理论(PLT，Programming Language Theory)专业的逻辑讲，它就是对语言本身的研究，能告诉你一个程序语言的本质是什么东西。当然了，研究得很深以后，对实际生活来说也许没什么必要，大多数人也不感兴趣。我只是想把最简单的东西讲一讲，(因为稍微难一点的东西我不会:p)，普及一些正经的课程或书不会提到的东西，讲一些刚学的时候很难理解，但理解以后会感觉“编程怎么这么简单”的知识。顺便一提，我希望最后能让读者学会所有程序语言 (不是要你们去学，而是看到一门新语言，马上就能分析出它的优缺点，类似这样的意思) 能学会各类语言的设计，或者说设计自己的语言。

现在的语言都有各种乱七八糟的东西，我想尽量讲的简单，让人不要丧失太多的信心。这就是这系列文章的目标。我还不知道我能不能做到。

给个例子吧，排序，大家都知道，但我一看见那两重循环就头疼，直到我学了 Scheme 语言:

(define (sort ls)
  (if (null? ls) null
      (let ([m (apply min ls)])
        (cons m (sort (remq m ls))))))

学过的人肯定会有意见，但我不是想显示一下有多简单嘛，第一行定义这个函数名叫 sort。第二行说，如果参数是空列表，结果当然也是空列表。第三行说，否则，就找列表中的最小值。第四行递归进去，就是以同样方式处理剩下的列表。程序写完了。你跟别的语言比一比就知道了。

(啊对了，感兴趣的可以去跟一个叫 APL 的语言比一比，现在不知道还有多少人听说过这门古老至极的语言，总之在有兴趣的时候，长长见识还是可以的:)

那是我第一次发现，写程序这么简单。就在那时我才对编程有了兴趣。以前学算法都只是死学而已。

我也啃过那本著名的算法导论，说实话，我觉得真正能看下来的不是一般人。为什么呢，那里面的代码…实在是太恶心了。我都只能看书上的图画，不看代码，因为书上的代码复杂到没法看。真的。我是那种见到麻烦的东西就泄气的人。比方说吧，我还记得书上红黑树的代码直到最后也没看下去，但是没关系，因为我后来就看到了一本 ML 的教材，它也讲到了红黑树，我一下子就明白了，ML 模式匹配和递归，跟伪 Pascal 代码简直不是一个等级的。

人使用的语言和接触的环境是会改变人的思考方式的。

追求简单就是我这些文章的目标。

长期以来，有个事一直在困扰我，那就是越昂贵的，越是前沿的，就越可能是没用的。然后，困扰我的另一个事是，电脑是一个死的机器，却可以不可思议地完成那些巧妙的事情，而程序员是那么聪明的人，却在做着不可思议的愚蠢的事情。简而言之，他们真是天生的一对。
—— Bill Bryson

(注：我感觉我前两节写得很烂，没什么创意，有谁有建议欢迎告诉我)

(因为大家都对数学比较熟悉，所以先从数字开始吧，记忆的内容会少很多。当然只要你知道加减乘除就可以了。有趣的东西在后面。)

首先，一个程序是什么？

举个例子吧，这是个什么也不干的程序，名叫 Program:

你给它一个数字，它再还给你。我们的电脑可以储存整数和大概十几位的小数。

在初学阶段不会遇到电脑存不下的数字的，请放心。

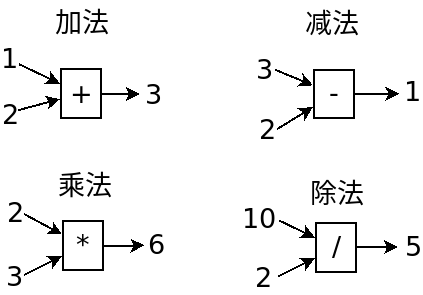
可以看出来，写着加减乘除的方框是一个神秘的机器，它吃进去两个数字，把结果吐出来。

(我们习惯用这4个符号表示加减乘除，因为它们能在键盘上直接打出来)

这其实就是四个简单的程序，它们都是你的电脑自带的，我们不用在乎它们对数字干了什么，反正得到了想要的结果，应该相信它们。

编程的过程就是把它们组合起来的过程。

你现在拿出纸(画图软件也行)，照着画一下 1+2*3，(1+2)*(3+4)，1+2+3+4

(谁也不能阻止你直接往下看，但题目不是我随便写的，请不要看得太快，我认为总会有人遇到问题的)

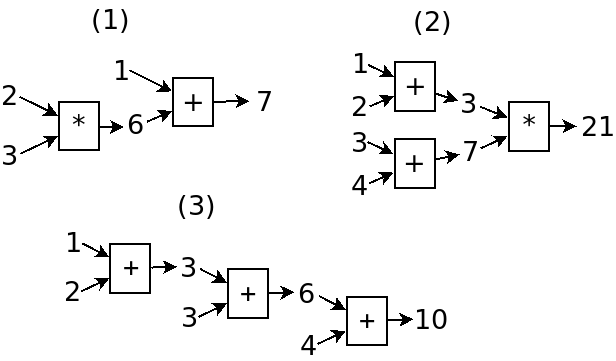
首先，需要留意的是，它们不是瞬间发生的，这是编程和数学最大的不同。数学只要式子和结果，不在乎它们的先后过程，所以数学可以解方程。但作为一个现实的程序，它永远有计算的顺序，我们不但关注它的结果，我们还关注它是怎么计算出来的。

计算 1+2*3，首先是 2 和 3 进入乘法程序里，等 6 出来之后，它和 1 一起进入加法程序。

第二个问题是，(1+2)*(3+4) 中，两个加法能否同时运行。你可以认为，它们是不能同时运行的，电脑里只有一个加法程序，它算完 1+2 之后，跑到下面去算 3+4，然后 3 和 7 一起进入乘法程序。当然，也可以先算 3+4，反正得一个一个算。

(现在的电脑多数都能自动同时计算这两个式子。(知道多核 CPU 的人别着急，这是单个 CPU 内的并行，跟你知道的东西无关) 但是这对你来说不重要。电脑爱怎么算它跟你无关，就算同时计算也只是把速度乘了个倍数而已，对我们来说，在乎这些东西没有意义。)

第三个图就有些微妙，有人可能有不一样的结果，可能是 (1+2)+(3+4) 而不是 ((1+2)+3)+4. 它们有什么区别自己思考。

再加一个思考题: 我们有没有漏某种情况？

虽然很烦人，但程序的问题就是这么出现的，考虑边边角角是个好习惯。至少需要知道，一个数除以 0 会怎么样。按照常识，程序会出错，就是这样。不多说了。

管理一群程序员就像放养一群猫
—— 无名氏

所以管理一群数字…(瞎扯)

比方说，要计算复杂的公式，或者有重复的式子，比如 1+2 的平方:

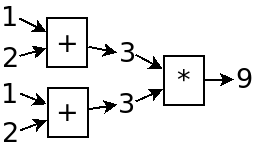
画两遍 1+2 就有些麻烦(好吧我是复制粘贴…)，还费时间费电，变量就出现了。
先定义个变量 three，然后让它平方。

你可能看不出来为什么要一个变量？完全可以在图里把 three 去掉，直接从左到右画两条箭头。那个 three 本质上什么都不是，只是给那两个箭头起了个名字罢了。变量在本质上就是给箭头起个名字，这样也许可以减少重复计算，不过多数时候也是为了让人更容易看懂。我为了把这个名字和程序区分开，用一个圆圈表示，但其实它什么都没干，只是传递了一个数据。

在实际程序中，即使没有重复的计算，也应该适当使用变量，并给它取个好名字，这样程序就更容易读懂了。变量的名字对电脑来说无所谓，只要不重复就行，只是对人来说就不一样了。

当然，一个变量只能储存一个数字。关于变量其实就这么多。

数学老师讲过什么叫函数。也许是这么说的:
y=x+1
这就是个函数。

可是在程序里就有点问题了，如果是这样:

那 y 只是个变量而已，比如这个程序的前面定义过 x 是 100，那么 y 就是 101，是一个固定的数字，如果 x 没有定义过，那程序就出错。

那什么是函数呢，你可以想象成一个机器，有入口，有出口，在内部对数字进行一些加工。简单来说，把 x+1 打个包就是个函数了。

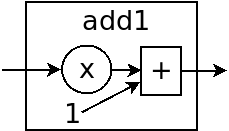
它左右的两根线就是入口和出口，这个 x 被包在了函数里面，然后被传给了一个加法程序，(1就是凭空出现的)，然后把结果传出去。在编程里，函数的输出一般被叫做“返回值(return value)”，或者干脆说函数的“值(value)”。

我这里只是把它画成了透明的，实际中是看不到函数内部的，所以我们给它贴了个名字叫 add1，告诉我们这个函数的作用。(叫它 y 或者 f 都可以，但因为这些名字没有意义，所以不推荐)

思考: 仔细对比之前学过的几幅图，你可能会发现什么。

第一个发现: 函数就是个小的程序，程序就是个函数。它们长得是一样的。这告诉我们，一个程序的本质不是一行行代码，计算的本质也不是按照代码一行一行算下来。一个程序只不过是得到一些输入，按你的要求计算一些东西，然后输出而已。(其实很早以前，函数(function)就被叫做子程序(sub-routine))

第二个发现: 函数长得跟加减乘除一模一样。也就是说，加减乘除其实就是函数! 你看，它们的概念也是一样的，输入、加工、输出。编程中函数的定义更广了，函数可以有任意数量的输入，而不只是一个。

从这里我们就大概能体会到函数存在的意义了，在电脑中，甚至一个加法都是很复杂的，你知道的，通过各种二进制的电路来实现，但是你学编程，不需要知道电路是怎么样的，只要使用加法函数就可以，那个加法函数的内部，其实是极其复杂的运算。

这就是函数的意义，它让你不用每次做加法都把复杂的二进制计算写一遍，而是一个加法函数搞定。你自己写的函数也是一样。

举个例子，sqr 函数是平方函数: sqr(x)=x²

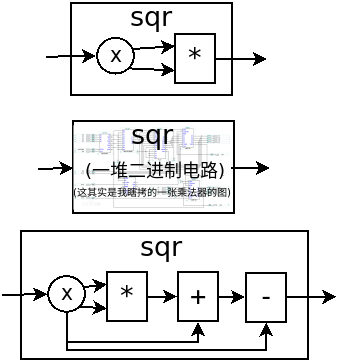
这 3 个函数的作者分别是正常人，一个疯狂的黑客，还有一个存心坑你的人，除了速度快慢，你并不能感觉出什么差异，反正你用的开心就可以。在写大一些程序的时候，这个作用就体现出来了。

我啰嗦这么多，看起来很简单，可是确实这点容易被忽视。刚开始学的时候，我们都没有把一块程序提取出来成为一个函数的意识，我看过的很多代码，比如要算 x² 并采用了第二种很复杂的做法 (比方说是为了提高一点点效率)，却不把它写成函数，看过去就是一大堆“…… x ……” 我要费很大功夫才能看懂他要干嘛。就因为这个，很多教科书建议大家写注释，就是在旁边注一句“这段代码把x平方”。可是只要写成函数，函数的名字就充当注释的作用了，这些麻烦就都没了。这也是函数的用处之一。把小的函数组合起来，最终能够形成一个大型程序，如果一开始就想着整个大型程序的代码，到最后肯定是脑子一团糟的。

需要注意的是，没有哪个好工程师会赞成写一个“摧毁巴克达”的函数。最基本的职业规范告诉他们，应该去写一个叫“摧毁城市”的函数，然后把“巴克达”当成这个函数的参数。
—— Nathaniel S. Borenstein

到现在我只画了图，因为那个图才是程序的含义，现在确实有这样画画图就可以编程的语言，但我都不满意，什么时候我有能力了可以考虑编一个这样的语言。但现在还是只能学要一行一行打代码的语言了。画图多形象啊，为什么大家都喜欢写代码呢。

(此括号内为扯淡时间，之后遇到这个情况可以返回来看一看，现在还是跳过吧~

当然，肯定还有人想问，为什么我非要用英文不可呢，中文难道不能编程吗。当然可以，你如果记不住英文，你就直接用中文字打变量名，没人会怪你。而且，如果记不住语言自带的函数名，你可以直接给它起别名，举个例子，(我经常这么干，当然对于 + 这种早就记住的就不用了)

(define 加 +)

甚至，你要是觉得几个特殊语法也记不住，你可以复制如下代码去试一下

(define-syntax-rule (定义 x ...)
  (define x ...))
(define-syntax-rule (函数 x ...)
  (λ x ...))
(define-syntax-rule (如果 x ...)
  (if x ...))

;; tests
(定义 加 +)
(定义 壹 1)
(定义 加一 (函数 (参数) (加 参数 壹)))

> (加一 壹)
2
;; 此处应有表情包

应该能看懂了吧

:)

我们要用的语言，叫 Racket，我斟酌过很久用什么语言入门会比较好，想起我以前抱着一本大厚书啃 C++ 时候的痛苦，我希望能找一个容易把问题讲清楚又好学的语言，可惜没有找到。虽然我对 Racket 还是不太满意，但毕竟没有什么明显的缺点，只要不被它的括号吓跑的话…

现在市面上有上百种语言，我接触过的至少有二三十种，最一开始一些概念没人也找不到书给我讲清楚，只能靠我反复看代码，猜它的意思。

我发现有程序语言这个专业是在初三，我开始看一些国外大学的教材，我接触到的最好的有 SICP、EOPL、The Little Schemer、The Seasoned Schemer 这几本书，SICP有官方的电子书，我整本打印了看，EOPL找到了盗版，因为上百美元真的不是我能付得起的…

也许我会推荐别人去看这些书，它们写的真的非常好，特别是 SICP 是我最喜欢的编程书，我以前在学校学了一年算法竞赛，又回家自学了两年(因为跟不上:p)。我一直以为编程就是算法。但当我翻开这本书时，我意识到原来我以前根本就不会编程。曾经很多抽象的概念在我心里都很模糊，我只会模仿，但是它用直观的图画和逻辑讲的极其清楚，我不但心里有了极其清晰的概念，用起来得心应手，而且甚至学会了实现它，学会了自己设计语言。

但其实我不会跟别人说，我自己看的时候，忍不住一直打盹，连着五六页满满的英文，实在不想看它在讲什么，要么就是连着五六页满满的代码，太痛苦了。

而且我不想被一门语言限制住，我尝试自己发明语言，融合我接触过的语言里面的优点，但我一个人实在是力不从心。一节课才40分钟，通常我思路还没整理好就下课了。所以，我最后还是无奈地选了一个我觉得最好的语言。至于你们觉得它括号太多，这个现在我也解释不了，只能以后你们自己慢慢感受了。

下面开始吧。

输入一个数字，Racket 就会原样输出。

> 2333
2333
> -123.456
-123.456

一般来讲，在电脑上看到这个大于号“>”，后面就是我们要输入的东西，输入之后按回车，电脑就会在下一行把结果显示出来。我为了程序看的清楚，如果一行写不下可以换行。

这是加减乘除，你可以试着在键盘上把这4个符号找出来。

> (+ 1 2)
3
> (- 3 2)
1
> (* 2 3)
6
> (/ 10 2)
5
> (+ 1 (* 2 3))
7
> (+ (* 1 2)
     (- (/ 4 2) 1))
3
> (+ (+ (+ 1 2) 3) 4)
10
> (+ 1 2 3 4)
10
> (* 1 2 3 4 5)
120

首先，加减乘除的格式是统一的，一对括号，括号中第一个是函数名，后面跟参数，用空格隔开。所以 (+ 1 2) 就是数学中的 (1+2)
函数可以嵌套，比如

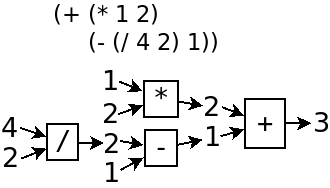
放心，以后不会有这么复杂的式子的。
(话说回来，也许代码比画图有个好处，因为代码稍微复杂点就看不清楚，所以它逼着人们写简单的代码。)

数学中的函数是有优先级的，但 Racket 里没有，而且也不能省略括号或乘号，也不能多加括号。比如我多加了个括号 (1)，但其中的1的位置应该是一个函数 (比如加减乘除)，但1不是函数，所以会出错。总之，就是完全的死板就对了。

刚开始学编程的时候我也很烦这个，因为打字麻烦死了 (不过相信我，你除非在编一道数学问题，不然一般是不会遇到这样复杂的数学公式的)。但现在我居然也开始慢慢欣赏这种死板的写法了，在我看过很多一大串的、根本搞不懂哪个符号是哪个的数学公式之后。相信我。

最后是 Racket 提供的一个便利的写法，因为连续相加和相乘很常用，所以加法和乘法可以有任意个参数。

这就是所有的数学内容。

定义变量:

> (define abc 123)
> (define this-is-a-variable (+ abc 1))
> abc
123
> this-is-a-variable
124
> (define abc 100)
出错，因为变量不能重复定义

定义变量的语法是 define，跟着要定义的变量的名字和它的值。

一个变量名可以是字母或大多数的符号(+-*/<>?=!%^ 之类)或数字连在一起，一般会用英文单词，习惯上中间用横杠(就是减号)隔开，让人看得更清楚。一个变量名字的左右都要有空格(或换行)隔开，所以这时的横杠并不会被当成减法函数。

思考: define 是函数吗？

那要先看看函数是什么。

一个函数，在调用之前应该先计算它的参数，比如 (+ (* 1 2) abc) (假设 abc 还是上面定义过的 123)，程序先计算 (* 1 2) 结果是2，abc 结果是 123，然后再运行 (+ 2 123)

如果 define 是函数，那么比如 (define x ...) 需要先计算 x 的结果，但这时候 x 还没有定义。显然是不对的。

define 只是一个特殊的语法。它只是定义变量这个动作，所以它也没有输出，只能单独写作一行。只是格式跟函数长得一样而已。

> (define m (define n 100))
出错，因为 define 只是个动作，没有输出
> (+ 1 (define x 100))
出错，同理

下面就是自定义函数了。

> (λ (x) (+ x 1))
#<procedure>

λ 开头的式子是一个函数，接下来是一个括号，括号里是参数的名字，再接下来是函数输出的值。很明显，λ 也是个特殊语法。

(不会直接打出 λ 的话，可以用 lambda 代替，你在其它地方看到的程序，一般也都会用 lambda，之后就不提这个了)

顺便一提，它会输出 #<procedure> 而不是原模原样的 (λ (x) (+ x 1))，就是因为这个函数内部已经看不见了。因此所有的函数在我们看来，都是一样的 #<procedure>

函数也可以有任意个参数，比如

> (λ () 1) ;; always 1
#<procedure>
> (λ (x) (* x x)) ;; square (平方)
#<procedure>
> (λ (pi radius) ;; area of circle (圆面积)
    (* pi radius radius))
#<procedure>

跟在分号后面，颜色不一样的，是程序的注释，会被计算机忽略，它们就是专门写给人看的，之后我会用注释来简单解释程序的意思。

上面只是写了几个函数，但就像只写个数字一样，你得把它定义给变量，不然它并没有被定义，输出以后就消失了。

> (define always1
    (λ () 1))
> (define sqr
    (λ (x) (* x x)))
> (define circle-area
    (λ (pi radius)
      (* pi radius radius))) ;; 或者 (* pi (sqr radius))

现在我们定义了3个新的变量。

你可能又发现了，定义函数的语法跟定义数字变量是一样的，只是后面跟数字还是函数的区别。现在，变量的含义增加了。变量可以储存一个数字或者一个函数。

调用函数也是一样的，括号中第一个是函数，后面跟它们的参数，你会发现它们和加减乘除的格式是统一的。

> (always1)
1
> always1 ;; 注意跟上一个的区别
#<procedure:always1>
> (sqr 3)
9
> sqr ;; 数学上总是用 (sqr x) 表示这个函数，
      ;; 你会发现是多么错误的一个写法，
      ;; 请自己好好思考一下这个问题
#<procedure:sqr>
> (circle-area 3.14 10)
314
;; 等价于直接用 λ 替换
> ((λ (pi radius) ;; 最外面的括号是函数调用
     (* pi radius radius))
   3.14 10)
314

就跟数字可以直接写出来，不一定要定义给变量一样，函数也可以直接写出来用，只是看起来比较复杂。

我们定义和使用一个函数其实是这样的，它们在计算机中都只有一个，但是存进变量以后，什么时候使用它，变量就把它拿出来，跟拿出一个数字一样。

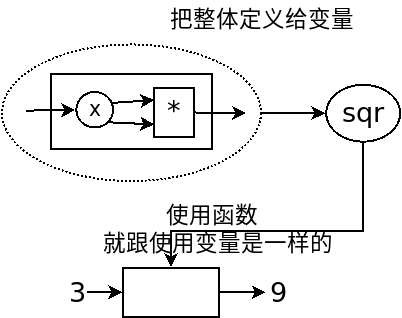
因为这么画太不方便，所以才画成函数上面贴个名字。

课外知识:
有人可能会好奇函数是怎么存进变量里的，答案就是，变量存的其实还是个数字。
比如地球上任意的位置都可以用数字(经纬度)表示，用 GPS 可以定位，电脑里也是这样。函数也是一段程序，它也是储存在电脑里的，所以它在电脑里有一个地址，这个地址就像经纬度一样，是个数字。我们要调用这个函数，只要知道它的地址，就可以找到这段程序，然后运行，就是这么简单。
现在不用在意这些细节问题，等到接触操作系统及以下的底层知识的时候，会很详细地讲这些东西(说实在底层的知识挺无聊的，还是高级一点的语言有意思)

思考题: 你知道为什么数学老师告诉你，计算一个式子，要先计算最里层的括号吗？

当然可以从最外层的括号开始算。不可能算不出来的。你明白这个吗？就算我们不从最内层括号算，而是调用外层函数的定义，我们也能算。

> (sqr (+ 1 2))
=> (* (+ 1 2)
      (+ 1 2))

只要你在不停地算，就一定能算出答案。接下来的步骤可以是

> (* (+ 1 2)
     (+ 1 2))
=> (* 3 (+ 1 2))

然后再下一步呢？

我们可以先把剩下那个 (+ 1 2) 算出来，然后计算 (* 3 3)

但也可以套用乘法的定义，先算乘法，把 (+ 1 2) 整体带着

> (* 3 (+ 1 2))
=> (+ (+ 1 2)
      (+ 1 2)
      (+ 1 2))

你以前也许都没想过这回事。然后呢，我们可以接着随意地算，直到算出最后的答案 9

但问题其实在于，这样的效率实在是很感人呐。我们到底算了多少次 (+ 1 2)，有谁帮我数一下…

如果把 (+ 1 2) 换成一个非常复杂的式子，那就更夸张了。所以你明白了，并不是什么不能算的问题，而是效率的问题。

而且之后我们会接触到更神奇的东西。你会发现，我们每次都着急地先算括号内的东西，其实是太勤奋了，我们有时候要懒一点才行，先把式子带着，先进函数里，必要的时候再算。不过这是后话了。

如果别人再扯什么括号之类的话，你心里应该明白，括号只是符号上的东西而已，由我们画的那些图，产生的想象，才是本质上的东西。

我现在可以解释程序语言专业的目的了，它研究程序表面和本质的关系，表面的符号是如何转化成本质的计算的，如何设计易懂的符号，诸如此类。

最后的问题就是，函数参数的名字。

比方说我还是跟计算圆的周长和面积，我把函数再重新列出来。

> (define pi 3.1415926)
> (define circle-area ;; 圆的面积
    (λ (pi radius)
      (* pi radius radius)))
> (define circle-circumference ;; 圆的周长
    (λ (pi radius) (* 2 pi radius)))

这里出现了3处 pi，但大家都知道这3个 pi 没有任何关联，circle-area 和 circle-circumference 的参数不会暴露在外面，所以即使调用 circle-area 和 circle-circumference 也不会导致 pi 被重新定义。

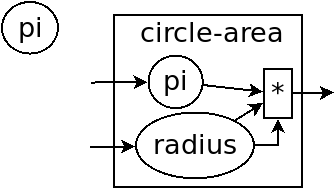
函数 circle-area 和 circle-circumference 中定义的 pi 都在函数内部，电脑遵循就近原则，函数内有 pi 了，就不去函数外找了。如果没有，再找函数外的，比如

> (define circle-area-v2 ;; another version
    (λ (radius)
      (* pi radius radius)))
> (circle-area-v2 10)
314.15926

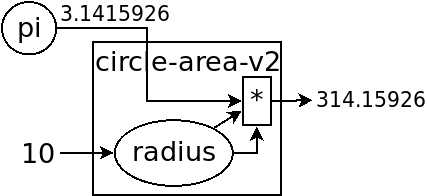
程序并没有出错，因为我们已经在外层定义过 pi 了。这个函数发现它要使用 pi，但它的参数没有 pi，于是它就到外面去找，发现 pi 是 3.1415926，于是使用了这个值。

如果函数外也没定义 pi，那就只能出错了。

可以想一下这样做的好处。很多时候，程序里有很多很多变量，比如各种常数和各种函数，大一点的程序是很多人一起写的，每个人都不知道别人到底定义了什么，要阻止重名是不可能的事了。

很容易想到的就是，我使用一个变量(包括调用一个函数)，如果我定义过了，那就先用我的，不用管别人定义了什么。问题就解决了。

思考: 上面的做法有 bug，不知道你能不能看出来
注: 这是一道超级难题。去看看历史就知道它花了科学家多长时间。直到现在还有些语言有这个问题。比如我现在正在 emacs 上写这篇博客，它用的语言 emacs-lisp 就是这样的
提示: 调用 circle-area-v2 函数。

看看这个函数吧。

;; (define pi 3.1415926)
;; (define circle-area-v2
;;   (λ (radius)
;;     (* pi radius radius)))
> (define cylinder-volume ;; 圆柱体积 = 底面积 × 高
    (λ (pi radius height) ;; 这个 pi 会覆盖外界的 pi
      (* (circle-area-v2 radius) height)))
> (cylinder-volume 3.14 1 1)
3.1415926 ? 3.14 ?

现在的问题来了，circle-area-v2 中的 pi 到底是哪个 pi，是最外层的常数，还是 cylinder-volume 的参数？

(你最好拿张纸把这几个函数抄一下，在纸上打打草稿，不然光看要晕倒的)

先讲现在已经抛弃了的方法。

照我们前面的解释，调用 (cylinder-volume 3.14 1 1) 之后，离 circle-area-v2 更近的 pi 变成了 3.14，而不是外界的 3.1415926，所以结果是 3.14。

或者，因为 circle-area-v2 是 (λ (radius) (* pi radius radius))，所以把 circle-area-v2 用它的值代换，cylinder-volume 就等价于

(λ (pi radius height)
  (* (* pi radius radius)
     height))

所以答案就还是神奇地变成了 3.14。

所以许多最古老的语言就都是这么做的，因为看起来理所当然。

但理所当然是不行的，对一个语言来说，实用才是关键。所以还要看看它靠不靠谱。比如 circle-area-v2 是我写的，我为了方便，定义了个变量 pi，然后在 circle-area-v2 里用了 pi，然后把代码发给了你，你上来就写了个 cylinder-volume，你看了看，circle-area-v2 只有一个参数 radius，也就是说圆的面积只跟输入的半径有关。所以我如果一直输入半径为 1，结果也应该永远是个定值 (circle-area-v2 1)，即 3.1415926。结果发现 (cylinder-volume 3.1415926 1 1) 是 3.1415926，(cylinder-volume 3.14 1 1) 是 3.14，很不对是吧。都是 (circle-area-v2 1)，结果居然不一样。这还怎么写代码。

那我也很不爽啊，我好好地定义了个 pi，结果被你的给覆盖了。

(可能有人觉得，没人会在 cylinder-volume 里定义 pi 却不用，那我大不了就用一下呗，比如我要一个高就为 pi 的圆柱。
非常实际的例子暂时举不出，但真的太多太多了，但我暂时真的想不出来这种难度的例子了/(ㄒoㄒ)/~~)

总归事实已经证明了，这对一门语言带来的几乎都是灾难。

于是有人提出来，我们说“最近的变量”，不应该是在使用的时候最近，而是在定义的时候最近。circle-area-v2 在定义时，pi 就是 3.1415926，这才应该是离它最近的那个 pi，那它就应该保存那个 pi，它的 pi 就应该一直是 3.1415926，而不会随着使用时外界的 pi 而变化。

现在一个函数不只包含一段程序了，它还要包含它定义的时候，所有用到的变量存放在哪里(地址)。

> (λ (...) ...)
#<procedure>

现在能理解为什么函数只会显示个 #<procedure> 了吧。

函数里包含了一堆东西，没法把它显示出来，只能用个 procedure 糊弄你一下。但这确实就是函数的全部了。

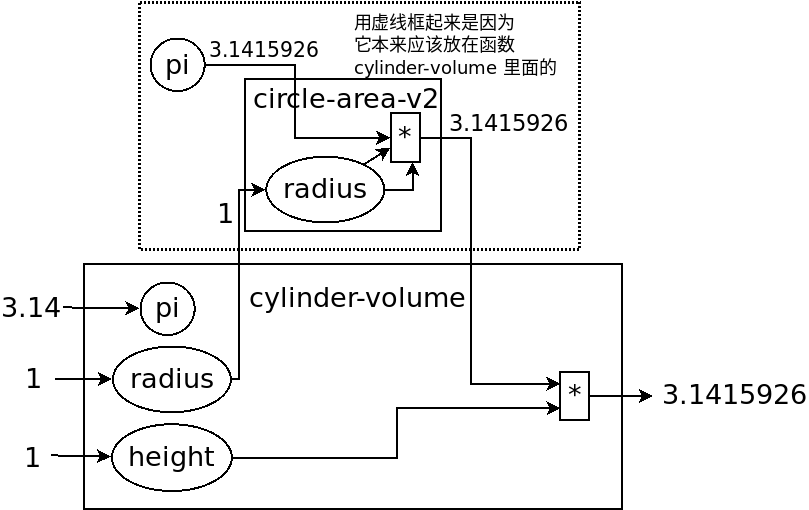
现在再看看我们画的图(伟大的美术作品…)，就不会出现这种问题。很清楚，我们画下这个函数的时候，就已经确定了所有变量的来源。实际上在图中，完全可以把变量的名字去掉，只画没有名字的圆圈就行，因为使用变量不需要通过名字，只需要知道它在哪就可以(前面所说的地址)，这就向机器语言又进了一步。

对于想知道术语，去网上查资料的人: 现在的做法叫静态作用域(static scoping)或词法作用域(lexical scoping)，过去的做法叫动态作用域(dynamic scoping)。因为过去变量是在函数调用的时候找的，是“动态”查找的。现在定义时候变量就确定了，是“静态”的。

这节是前面的一个复习。写几个简单的函数。

(define add-chip
  (λ (x)
    (+ 1 (* 10 x))))
;; test
> (add-chip 666)
6661

这个函数把一个数字的末尾加一个1。因为1就像一根薯条一样，所以起名为 add-chip (我要装作一本正经的样子)

同理，你可以想到我要干什么事

(define add-pie
  (λ (x)
    (+ 0 (* 10 x))))
(define add-peanut
  (λ (x)
    (+ 8 (* 10 x))))
;; test
> (add-chip (add-pie (add-peanut 0)))
801 ;; 请自己想象一下函数调用的图像

(这应该是个容易让你变胖的甜点)

当然，你也可以写出更多这样的函数，但是写的多了，你可能就发现你在写很多重复的东西，因为这些函数都是 (λ(x) (+ ? (* 10 x)))。注意，复制粘贴不是什么好办法，我们可以写出一个通用的函数来代替它们。

(define add-what
  (λ (what x)
    (+ what (* 10 x))))
;; test
> (add-what 1 666)
6661

请仔细体会一下这个函数是怎么写出来的，我们把会变的部分写成了一个参数。

请画一下下面这幅图像，最好把3个函数画在一条水平线上，要求是画得尽量好看。

> (add-what 1 (add-what 0 (add-what 8 111)))
______ ;; 请填空，3个数字的顺序注意不要反了

当然，这个函数是通用了，但是代码变麻烦了，那么也很简单，用这个函数定义之前的3个函数就行了。把之前的定义修改成如下

(define add-chip
  (λ (x)
    (add-what 1 x)))
(define add-pie
  (λ (x)
    (add-what 0 x)))
(define add-peanut
  (λ (x)
    (add-what 8 x)))

这些定义看起来会比原来的简单一些。

请再次体会一遍这个思路。

首先，我们知道如何在一个数后面加一个数字，这种数学知识是底层的细节，在写代码的时候，最好总是假设别人不会这个细节，比如别人对数学一无所知。嗯…

所以我们写了一个通用的函数 add-what 来表示这个细节，这样只需要调用它就可以了。然后直接使用它也可以，如果有些参数使用得比较频繁，那就自己再定义几个特殊的函数，add-chip，add-pie，add-peanut。

其实编程基本上都是在干这种事。从最底层开始，逻辑元件把二极管三极管 什么的物理知识隐藏起来了，集成电路把逻辑知识隐藏起来了，操作系统把硬件隐藏起来了，而我们用的语言又把系统级别的操作隐藏起来了。就这样一层一层，让我们更关注于我们要写的程序，而不是底层的这些东西如何工作。

这有一个名词，叫做“抽象(abstraction)”。

这里的抽象不是指让人难理解，相反，它指的是把底层复杂的东西隐藏起来，比如，完全不会数学的人也能调用 add-what，他会发现他的数后面神奇地添加上了另一个数字；完全不懂电路的人也会玩电脑；也有许多不懂物理的 3D 游戏程序员…… 我们不知道它们内部是什么，但不知道这些对我们没有影响，甚至更方便了。理解抽象是怎么回事也可以算是编程的内功吧。

这章讲如何安装 Racket，懒得搞这些东西的话可以直接跳过。

我故意跟别的教材不一样，其它的书都先让人安装各种软件，这样就可以在电脑上一边看书一边试验了，这是好事。但是，我发现一直待在电脑前，让我养成了一个很坏的习惯: 当我思路还没理清楚时，就迫不及待地想到哪写到哪，最后把整个程序搞得很糟，只能反复找 bug。相反，如果我手头没有电脑，我就只能在纸上打草稿，草稿就不那么容易随便修改，所以必须让程序在脑子里完全成型了再写下来，最后把它打到电脑里，一次性就是完全正确的。

电脑本来就只是辅助你运行程序的，如果自己没有完全理清思路，就不要指望电脑能得出正确的结果。

还要说的是，你用什么样的电脑，什么操作系统，你的打字速度，都是完全没有关系的。一定要用你最熟悉的操作系统，或者你的朋友/同学/同事用啥你就用啥。我看到有些教程一上来就让你装 Linux 和各种开发环境，有人折腾半天还没开始编程，感觉自己连电脑也不会用，还是别想着编程了，这真的是很糟糕的。(但是如果你还在用 Windows XP，我无法保证你能安装，因为 XP 实在太老了，现在几乎装不了什么软件了，建议换个新操作系统吧，我也不知道为什么在中国还有一些人在用这么老的东西。)

首先，Racket 官网是这个 https://www.racket-lang.org，你也可以直接去下载页面 https://download.racket-lang.org，默认下载就可以。如果你不熟悉，一路默认安装就可以，安装完以后你的桌面上就会出现 DrRacket 的快捷方式了。(像我一样用 Ubuntu 的可以直接通过 apt 安装 sudo apt install racket，DrRacket 会添加在你的应用里面。当然也可以用 Emacs 来编辑 Racket，我一直用的是 racket-mode，自己稍稍配置一下 paredit-mode 什么的，用起来还是挺舒服的。)

打开 DrRacket 以后，首先就在文件第一行打上 #lang racket，然后在后面就可以写代码了。具体不会操作的请直接上网搜，“如何安装/使用 DrRacket”

然后一定要记得切换到英文输入法，因为中英文的标点符号都是不一样的。

接下来就可以玩耍了。

在 定义窗口(definition window) 写一些变量定义，然后点屏幕右上角的 run 或者按 F5，就可以运行定义的内容，然后在 交互窗口(interaction window) 输入一些东西的计算。(具体怎么操作网上有详细教程，我懒得说了)

总共就这些要讲的，但如果你觉得不够，我就再说一些杂七杂八的内容。这些就别记了，知不知道都无所谓，就当了解一下了。

先说一些数字计算

> (/ 7 3)
7/3
> (/ 7 3.0)
2.3333333333333335
> (expt 2 100) ;; the 100th power of 2
10715086071862673209484250490600018105614048117055336074437503883703510511249361224931983788156958581275946729175531468251871452856923140435984577574698574803934567774824230985421074605062371141877954182153046474983581941267398767559165543946077062914571196477686542167660429831652624386837205668069376
> (sqrt 2) ;; square root
1.4142135623730951
> (cos (/ pi 3))
0.5000000000000001
> (exact->inexact 7/3)
2.3333333333333335
> (inexact->exact 2.3333333333333335)
5254199565265579/2251799813685248
> 1.23e5
123000.0
> 2e20
2e+20
> 2e-4
0.0002

1. Racket 支持分数表示，分子和分母只能是整数。
2. 如果是小数运算，结果也是小数，但小数计算的最后几位会不精确。
3. 乘方函数和平方根函数
4. Racket 提供了三角函数和 pi 的定义，对，前面我们自己定义的 pi 离我们更近，所以把 Racket 提供的给覆盖了。
5. 接下来两个函数是在精确值(整数、分数)和不精确值(小数)之间转换的。
6. 一个数后面紧跟“e”再加一个整数表示科学计数法，比如 1.23e5 就是 1.23×10⁵

还有很多各种各样的变量和函数可以使用，好奇的人请上网搜索或查官方文档，虽然我觉得如果是初学的话可能看不懂…

最后，既然已经没的讲了，我就随便编一个 sqrt 函数，自己实现一个简单的开平方根的函数。我实在不想推导数学公式，你们会什么方法就用什么方法吧。

比如我们要求 \(\sqrt{a}\)，我们设 \(f(x)=\cfrac{a+x^2}{2x}\)，然后随便取一个初始值，比如 1，然后一直调用 \(f\)，就像 \(f(f(f(...f(1))))\)，得到的结果就会越来越接近于 \(\sqrt{a}\)。(公式显示不出来的请反馈给我)

因为我们现在还没学更多的内容，我们只能让 f 接受两个参数，a 和 x，所以

(define f
  (λ (a x)
    (/ (+ a (sqr x))
       (* 2 x))))

然后 sqrt 函数也很简单了，就是一直调用 f 而已

(define sqrt
  (λ (a)
    (f a (f a (f a (f a (f a 1)))))))
;; tests
> (sqrt 4)
926510094425921/463255047212960
> (exact->inexact (sqrt 4))
2.000000000000002
> (exact->inexact (sqrt 2))
1.4142135623730951

可以看得出来，对于比较小的数，结果还是比较准确的。

比较有意思的一点就是虽然 f 接受两个参数，但它们是有主次之分的，a 只是一个附加的材料，而 x 像是主要的产品，一直顺着 f 流动。你可以自己画一下图试试。

目标: 能看懂这一章提到的语法，自己随便想几个简单的函数写一写。

安装了 Racket 的人一定要亲手打代码啊

自己写一遍平方函数，在省略号中填空

(define sqr
  ....)

同样，3次方和4次方

(define cube ;; 3次方
  ....)
(define power4-v1 ;; 4次方，版本1，只用乘法
  ....)
(define power4-v2 ;; 版本2，用 sqr 函数
  ....)

(如果有谁想出来了4次方更好的名字，请告诉我一声)

测试一下

> (cube 0)
0
> (cube 1.234)
1.879080904
> (cube 10000)
1000000000000
> (cube -10)
-1000
......
......
;; 正数、负数、整数、小数
;; power4 同理

虽然现在代码简单，这种测试确实没必要，这只是教你一个测试的好习惯，不要漏了什么
(但其实说不定就发现自己哪里打错了)

把下面代码的图画出来

> (power4-v1 3)
81
> (power4-v2 3)
81

附加题: 假设每次乘法的时间相同，函数调用不需要时间，能看出效率的差异吗(就相当于比较乘法次数)？ 如果是 power8，power16… 呢？

数学好的人很快就明白了吧，以后写了通用的乘方函数，再来详细地讨论这个问题。

还有一个值得深思的问题。

来看一下这个函数

(define run-forever
  (λ ()
    (run-forever)))

你可以试验一下，请务必记得 DrRacket 的右上角 Run 按钮的边上，有个按钮叫 Stop。

上面这个是下一章会讲的内容

最后是一个大概下下下章会讲的内容，很有趣的东西，先随便剧透一点。

既然函数可以像数字一样传递，那是不是也可以作为函数的参数和返回值呢

举个例子，

(define value-at-100
  (λ (f)
    (f 100)))

我们可以这样使用

> (value-at-100 sqr)
10000

这会有点颠覆你的想象，用它可以干很多有趣的事。

又是个无限循环

> ((λ (x) (x x))
   (λ (x) (x x)))

手动模拟一下吧，应该会发现每次调用完了都是不变的，所以会无限循环。

函数组合

(define compose
  (λ (f g)
    (λ (x)
      (f g x))))
(define add1-and-sqr
  (compose sqr add1))
> (add1-and-sqr 4)
25
;; 相当于 (sqr (add1 4))

哈哈，现在看不懂无所谓，注意 compose 里的第一个 λ 是定义为 compose 的这个函数，第二个 λ 是函数输出的值。

这只是最简单的。你信不信只用函数就可以实现数学的一切？从数字开始到各种数学运算，甚至逻辑运算(如果、与、或等)都能变成一个函数。感兴趣的参见 Church Decoding

剧透有点多了，就到这里了。

(评论系统不太靠谱，我又删掉了，以后看情况再加吧)