PL教程第二章停下来!

不同的包装
如果有如果的话
练习: 再来一瓶，再来一瓶
跳入梦中
私有财产

首先声明一下，虽然对数字加加减减没什么意思，但要是一上来学别的东西会更吃不消，把这些基本概念学好了以后，大约下一章就可以摆脱数字了。

不同的包装

猜一猜这是什么

> (= 123 123)
#t ;; t 代表 true，中文一般叫做“真”
> (= 123 100)
#f ;; f 代表 false，“假”
> (> 123 100)
#t
> (< 123 100)
#f
;; 还有 >= 和 <=，它们都是函数

很明显，它们都是比较数字大小的，分别是等于，大于，小于，大于等于，小于等于。(不得不说，看起来实在是怪怪的，我直到现在也觉得很难看)

它们的返回值都是 #t 或 #f，这两者又是跟数字、函数一样的东西，被称为布尔值(boolean)。(比如说 123 是数字类型，#t 和 #f 就是布尔类型)。我们把数字类型、布尔类型、函数类型，和之后会接触到的其它的类型，统称为“数据类型(data type)”

Racket 居然没有不等于函数，但有 not 函数，作为练习，请自己定义一下不等于函数。

> (not #t)
#f
> (not #f)
#t

(define =/= ;; 如果有谁想出了更好看的符号，告诉我一声
  (λ (x y)
    (not (= x y))))
> (=/= 1 2)
#t

然后观察一下这些函数，它们跟我们之前讲的函数有些不一样。

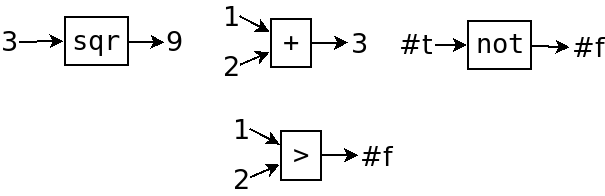
第二行的那个函数不同，不是因为返回值从数字变成了布尔。
而是因为它们把数字和布尔，这两种不同的类型混合起来了。

从上一章的内容中可以体会到，函数都好像工厂里，流水线上的机器一样。产品从一边流入，经过加工(有些是对一个产品加工(一个参数)，有些是把一些产品揉在一起(多个参数)，有些是多个参数，但有主次之分)，经过加工，把加工后的产品送出来。把函数组合起来就能完成程序。

但这些函数与之前所说的概念不太一样，它们只消耗了输入，但没有对它们加工，而是输出了一个判断条件，这是为了控制程序之后的走向。所谓的布尔值 #t 和 #f 就是因此诞生的。

来看一下如何使用它们

> (if #t 1 2) ;; 若 #t 则 1 否则 2
1
> (if #f 1 2)
2
> (if (= 100 100)
      (* 1 2 3) ;; 只要是值的地方都可以换成函数运算
      456)
6
> (if (>= 123 456)
      (not (= 1 2))
      (+ 1 2)) ;; if 的两个分支的类型不同也可以，
               ;; 虽然一般来讲没什么意义
3

if 类似于有3个参数的函数，第一个参数是判断条件，后两个参数是两个分支。第一个参数必须为 #t 或 #f，如果为 #t 则值为第二个参数，如果为 #f 则值为第3个参数，受到其它语言的影响，习惯上记忆为:“如果…那么…否则…” (if...then...else...)

不过要注意的是，if 不是一个函数。还记得吗，函数在调用之前，要先把参数都算出来。但很显然，if 不需要。如果第一个参数为 #t，那么只需要计算第二个参数就可以，第三个参数不管是多复杂的式子，都可以直接扔掉。如果第一个参数为 #f 那就只要计算第三个参数。所以 if 被设计成了一个特殊的语法，而不是一个函数。

练习题: 写出绝对值函数 abs，如果是正数或零则不变，负数则变正数。补充: - (减法函数)可以只有一个参数，(- 123) 为 -123

答案有很多种，这是其中一种答案:

(define abs
  (λ (x)
    (if (>= x 0)
        x
        (- x))))

继续练习题: 写出 max 和 min 函数，都接受两个参数，分别返回参数中较大的一个和较小的一个。

如果熟悉语法了就可以了。

我们还可以把 if 用于检查错误。比如说，如果给上面的 abs 函数输入一个布尔类型的值

> (abs #t)
; >=: contract violation
;   expected: real?
;   given: #t
;   argument position: 1st
;   other arguments...:
;    0

这个错误信息表示我们调用了 >= 函数，然而它出错了(contract violation)，下面几行就是，它要一个实数(real)，然而我们给了它一个 #t，是它的第一个参数，它还有一个参数是 0。现在看不懂这些没关系。反正这会让使用者很奇怪，为什么我调用了 abs 但给了我一个跟 abs 毫不相关的错误？

所以在实际中，一般都会自己检查这类错误，防止让使用者知道，你这个函数原来偷偷调用了 >= 函数。

(define abs
  (λ (x)
    (if (number? x)
        (if (>= x 0)
            x
            (- x))
        (error "abs: number expected, given:" x))))

(注: 严格来说应该用 real? 而不是 number? 是因为 Racket 里的数字可以是虚数，但反正你又用不到虚数，不用管它)

这里有好多新东西，一点一点来看。

首先，number? 是一个函数，判断参数是否为数字，跟它相似的还有 boolean? (是否为布尔类型)，procedure? (是否为函数)， string? (是否为字符串)，字符串下面就讲。

如果 x 为数字，那么就照常计算 x 的绝对值，如果不是就报错。

error 怎么说呢，它也是个函数，但跟一般的函数意义上又不一样了，一旦调用这个函数，不管你在程序的什么位置调用的它，程序都会直接出错。它的参数就是出错信息了，第一个参数一定要是个字符串，剩下可以有任意个参数，随便什么都可以，统统是出错信息。

至于字符串。我们把一个字(母)叫做一个“字符”，而一串字符就叫“字符串”。下面这些都是字符串

> "abc"
"abc"
> "this is a string" ;; 可以有空格
"this is a string"
> "" ;; 空的字符串
""
> "!@#$%^ &*()~ `[]-=';" ;; 基本上什么符号都行
"!@#$%^ &*()~ `[]-=';"
> "(+ 1 2)" ;; 这跟程序的 (+ 1 2) 一点关系都没有
"(+ 1 2)"

字符串就是用来表示一段文字的，两边双引号，里面的东西会全部当成文字，而不是程序。所以它会原样输出。一般只会用在给人看的一段文字中。

这样就讲完了，试验新的 abs 函数

> (abs #t)
; abs: number expected, given: #t

全部搞定。

再补充一下，= 这个函数只能判断数字相等，如果要其它类型，分别可以用 boolean=?，string=?，没有 procedure=?，因为两个长得一模一样的函数是不相等的，原因见上一章。为了避免误导，就没有提供这个函数。

> (define f
    (λ (x) (+ x 1)))
> (define g
    (λ (x) (+ x 1)))
> (equal? f g)
#f

但有一个通用的函数 equal?，所有的类型它都可以比较是否相等。所以如果你们懒得去记各种函数的名字，就记个 equal? 就行了。一般用 = 或 string=? 这些特殊的函数，只是为了强调参数的类型而已。对程序一般没多大影响。

这小节可能要记的东西比较多，但不用着急去记，暂时能看懂就行，慢慢就记住了。

练习题: 还记得上一章中的 add-what 函数吗，不记得的话回去翻一下 (传送门)。仿照上面的 abs 函数，检查 add-what 的 what 参数，确保它为 0~9 之间的整数。
注: 检查整数可用 integer?，小于或大于号也能有多个参数，比如 what 在 0~9 之间，可以写做 (<= 0 what 9)
请尽量写出让人能看明白的错误信息，并测试。

如果有如果的话

好了，现在是你在编程道路上的第一个难点。

好些时候，我们会需要重复做某些事，比如，又是上一章中的 add-what，一个 pie 两个 pie 差不多是够了，但对于 add-chip 来说，有没有一个函数可以一次性加上很多个 chip 呢？

(define add-many-chips
  (λ (num x)
    ....))
;; 在 x 上加上 num 个 chip

你的第一反应很重要。

(如果你数学真的很好的话，你也许会发现，num 个 1 就相当于 num 个 9 再除以 9，然后 num 个 9 等于 10^num 再减 1，如果你以为你就这样成功了的话，那请你自己写一下乘方函数，然后你就遇到同样的问题了)

你可以慢慢尝试一下，

请暂停阅读。

你最后可能会发现，要是代码无限的话，只能这么写

(if (= 0 num) x ;; 什么都不加
    (if (= 1 num) (add-chip x) ;; 加1个
        (if (= 2 num) (add-chip (add-chip x)) ;; 加2个
            (if (= 3 num) .... ;; 加3个
                ....)))) ;; ......

接下来就是找规律时间。我们已经知道，num 是多少，就调用多少次 add-chip，但要把它向电脑表达清楚。

那么问题就是，什么叫做“调用 num 次 add-chip ”？

经过研究，我们发现我们没法把 num 个 add-chip 写出来，但是我们看看上面的那一堆 if，我们发现了规律:
如果 num 多了 1，那么 add-chip 也多调用 1 次。

有人说，这不是废话吗。但这就是“调用 num 次”的本质。

我先不多说，但你可以从现在开始思考一下，自然数是怎么来的。其实你小时候，数数的时候，就明白了，但现在又忘了而已。

数字就是这么数出来的。

最一开始，你还不会一次性跳到某个数。比如要你数一排苹果，你会用一只手点着苹果，一边计数:
“一个苹果”，然后指到下一个苹果，
“两个苹果”，然后指到下一个苹果，
“三个苹果”，……

如果 num 是 0 呢？add-chip 调用0次。
如果 num 比 0 多 1 呢？add-chip 多调用 1 次，就是 1 次。
如果 num 再比 1 多 1 呢？add-chip 再多调用 1 次，就是 2 次。
如果 num 再比 2 多 1 呢？add-chip 再多调用 1 次，就是 3 次。
……

于是对任意的 num 都可以数了。

程序把上面的过程反过来就可以了。

(define add-many-chips
  (λ (num x)
    (if (= 0 num)
        x
        (add-chip (add-many-chips
                   (- num 1) x)))))

你可能会感到有些惊奇，为什么 add-many-chips 里面还能调用它自己。前面做了那么多铺垫，其实就是为了讲这个。

首先，来理解一下这段程序。如果 num 为 0，就直接返回 x，什么都不加; 如果 num 大于 0，就先调用 add-many-chips 给它加上 num-1 个 1，然后再加一个 1。

你问我为什么 (add-many-chips (- num 1) x) 神奇般地就完成了？因为如果 num-1 是 0，那它就完成了，否则就继续减 1，一直重复，直到减到 0 了为止。

我们需要从程序的角度详细解释一下。首先，我们都说它是“自己调用自己”，其实函数是没有自己调用自己一说的。你可以看成是有无数个函数，就像这样

(define add-many-chips1
  (λ (num x)
    (if (= 0 num)
        x
        (add-chip (add-many-chips2
                   (- num 1) x)))))
(define add-many-chips2
  (λ (num x)
    (if (= 0 num)
        x
        (add-chip (add-many-chips3
                   (- num 1) x)))))
(define add-many-chips3
  (λ (num x)
    (if (= 0 num)
        x
        (add-chip (add-many-chips4
                   (- num 1) x)))))
......

有无数个这样的函数。比如调用 (add-many-chips 3 666)

> (add-many-chips1 3 666) ;; 每一行都是一步调用过程
=> (add-chip (add-many-chips2 2 666))
=> (add-chip (add-chip (add-many-chips3 1 666)))
=> (add-chip (add-chip (add-chip (add-many-chips4 0 666))))
=> (add-chip (add-chip (add-chip 666)))
=> (add-chip (add-chip 6661))
=> (add-chip 66611)
=> 666111

我认为这样你是可以理解的，这就是普通的函数调用罢了。

画图就看得比较清楚了。直到现在，我自己还是这么想象它的。

比如说我们调用了 (add-many-chips 3 666)，首先，判断 num 是不是 0。(为了方便我竖着画)

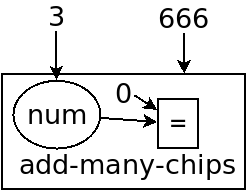
不是 0，所以先调用 add-many-chips，不过要记得完了还要加个 add-chip (有些箭头画不下了，省略了)

然后我们就要开始计算 (add-many-chips 2 666)，因为 2 不为 0，所以接着调用一层

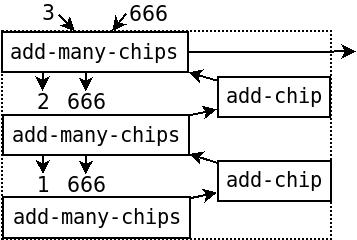
然后需要计算 (add-many-chips 1 666)，同理，1 不为 0，再调用一层

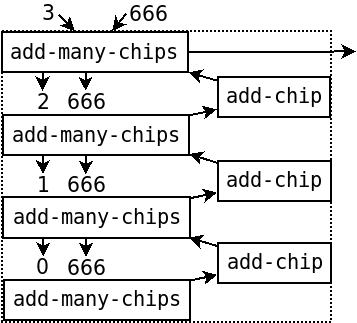
好了，现在最底下的这个函数终于发现它的参数是 0 了，于是它很高兴地返回了 666。

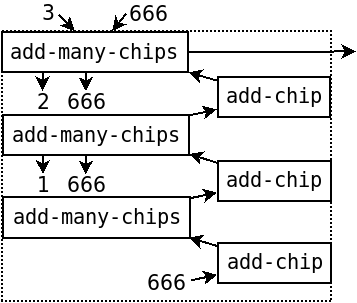
接下来就明白了，这个 666 经过了 3 个 add-chip 最后得到了结果。

有人可能想问，那在最下面的函数计算的过程中，上面的那些函数干什么呢？

干等着。每一个函数都在等下面的那个函数返回结果，好继续自己的计算。这不是只有调用自己才会这样的，普通的函数也是这样的。

现在你应该大致能想象出这个流程了。我以前看书自学的时候，所有的教程都是一上来就说“自己调用自己”，这本来就是个误导。然后又开始讲各种高级的概念，比如“栈”，让我看得一头雾水。就这么个东西，我大概整了两年才搞懂。上面就是我现在自己的理解。

我现在不想提计算机到底是怎么实现函数一层层调用的，反正就可以当它是自动发生的。不过我们依然可以看出，每调用一层函数，它就会多占用一些内存，比如每层 add-many-chips 函数中都有自己的 num 和 x 参数，当调用的非常非常多时，内存就存不下了。对于想知道术语的人: 这就叫做“栈溢出”。其它绝大多数语言里这个问题很普遍，因为栈是内存中固定的一部分。但 Racket 里就没有这玩意(除非你真的把电脑所有的内存都用完了)，这也是我用 Racket 的一个原因，你可以专心地学习，不用担心函数调用的次数太多这类稀奇古怪的问题。

所以我们可以来玩一下。

> (add-many-chips 10000 666) ;; 相信我，我真的打了 10000 个 1 上去，不信你拖滚动条自己数数:p
6661111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111

这在我的电脑上也是瞬间的事(DrRacket 中可能比较慢，是因为它把这个数字输出到屏幕上很慢，但开始输出的瞬间它就已经算出结果了)。电脑的速度真的比你想象中要快得多得多得多…所以我一直想知道，那些能让我的电脑变得很卡的软件究竟干了些什么…

思考题: (请先保存好你的代码，否则后果自负，不过除非你的操作系统抽风了，不然并不会影响系统和其它软件的，请放心)。给 add-many-chips 输入一个很大的数，内存可能就爆了，比如，我给了它一个亿…然后它 3 秒钟后占到了 3.2G 的内存然后卡住了…
好。这说明我们要量力而行，那给它一个小一点的数，比如 2.5 吧

> (add-many-chips 2.5 666)

为什么它又卡死了？

手动模拟。它要计算 1.5，然后 0.5，然后… -0.5，然后 -1.5，-2.5，…

同理，如果输入是负数的话也会死循环。

那就加点错误处理吧

;; 把原来的函数重命名为 add-many-chips-unsafe
;; 记得把函数里面调用自己的也重命名了
(define add-many-chips
  (λ (num x)
    (if (or (< num 0)
            (not (integer? num)))
        (error "add-many-chips: invalid first argument. expected: natural number, given:" num)
        (add-many-chips-unsafe num x))))

(define (or x y) ;; 只要参数有 #t 结果就为 #t，参数都是 #f 结果才为 #f
  (if x #t y))

当然，如果要详细地写，就还要先检查参数是否为数字，否则 (< num 0) 又会报错… 然后你就会被烦死。总之你永远也阻止不了别人错误地使用你的程序。

当然，你在用别人的程序时也一样，别人检查地再怎么仔细，如果你边打盹边打代码，就不要指望程序是正确的了。

以后我就很少再提错误检查了。因为代码这么短，动不动就检查反倒没必要。这节就这么结束了。

思考题: 有人可能认为没必要写两个函数，都写在一个函数里就可以

(define add-many-chips
  (λ (num x)
    (if (or (< num 0)
            (not (integer? num)))
        (error "add-many-chips: invalid first argument. expected: natural number, given:" num)
        (if (= 0 num)
                x
                (add-chip (add-many-chips
                           (- num 1) x))))))

第一，这段代码正确吗？

第二，如果正确的话，请手动模拟，比如调用 (add-many-chips 3 666)，两个版本分别检查了多少次错误？效率上是否会有不同？

练习: 再来一瓶，再来一瓶

(警告: 这章会用到一点数学知识，因为我实在想不出不用数学的例子了， 如果有谁想出来了请一定要告诉我一声)

像上一节中所说的，函数调用自己的这种模式有一个名字，叫做“递归(recursion)”。

准确来说，函数除了直接调用自己，还可以间接调用自己，比如 f 调用了 g，g 又调用 f。

上一节中也看到了，递归跟普通的函数调用是一样的，没什么特殊的。唯一的区别就是它可能导致程序死循环。因为它相当于你写无数个函数。

下面是两个练习

第一个是上节提到的乘方函数。

(define expt ;; b 的 n 次方，只考虑 n 为自然数
  (λ (b n)
    (if (= 0 n)
        1
        (* b (expt b (- n 1))))))

如果你还不理解函数的原理，请复习上一节。但只知道这个函数是正确的还没有用，还需要学会自己写。

要写 bⁿ，先来分析一下这个函数。首先，用自己能看懂的方式写出来

bⁿ = b*b*…*b，共 n 个 b

然后改递归(当然，你要先确定没有更简单的方式了。比如写 1+2+…+n，当然就直接套求和公式了)

首先，考虑省略号中是什么？

就是 n 个 b，没错吧。而 b 就永远都是 b 这个定值，所以对 n 递归。

所以 n 的范围是什么？

我们只考虑自然数，所以是 0,1,2,3… 这些数字。

接下来就要找到一个方法，让我们不管输入什么 n，程序都不会死循环。然后用这个递归方法，把函数写出来。

对自然数来说，大多时候都是每次减 1，一直减到 0，根据情况有例外，下面就会举一个例子。

好，那就根据这个递归方案，试一下能不能写出程序。

b⁰ = 1，这种情况很简单。
若 n>0，那么 bⁿ 要先调用 b^(n-1)，然后只要再乘个 b 就行了。
bⁿ = b*b^(n-1)

然后写成上面的程序就完成了。

繁琐的练习题:

如果把 b⁰ 的情况改成 b³ = b*b*b 会怎么样？
如果把递归的情况写成 bⁿ = b⁽ⁿ⁺¹⁾/b 会怎么样？
如果把递归的情况写成 bⁿ = b*b*b^(n-2) 会怎么样？
把递归的情况写成第3题所示，怎样让函数总能停止？(提示: 两次 if)

练习题:
写出阶乘函数: factorial(n)=1*2*3*4*...*n , n>=1

根据上面的方法，我们要把 1*2*3*...*n 改成一个递归式，比如先尝试 1*(2*3*...*n)，然后会发现失败了，因为 (2*3*...*n) 还是跟 n 有关，而不是跟 n-1 有关，所以会发现递归式应该是 n*(n-1*...*3*2*1) 即 n*factorial(n-1)

这样代码就完成了

(define factorial
  (λ (n)
    (if (= 1 n)
        1
        (* n (factorial (- n 1))))))
;; test
> (factorial 10)
3628800

练习题:
写出函数 first-digit，输出一个正整数最高位的数字。

> (first-digit 123)
1

考虑一下。如果是个位数，就直接输出。这就是递归终止的情况。

(define first-digit
  (λ (n)
    (if (< n 10)
        n
        ....)))

否则，它就至少是两位数，把它的个位删掉，然后重复同样的过程。

(define single-digit? ;; 是否为一位数
  (λ (n)
    (if (< n 10) #t #f)))

(define delete-units-digit ;; 删掉个位数
  (λ (n)
    (quotient n 10))) ;; n/10 取整

(define first-digit
  (λ (n)
    (if (single-digit? n)
        n
        (first-digit (delete-units-digit n)))))

;; test
> (first-digit 123)
=> (first-digit (delete-units-digit 123))
=> (first-digit 12)
=> (first-digit (delete-units-digit 12))
=> (first-digit 1)
=> 1

总有一次，我们删到了只剩一位数，这个数就是原来最高位的数字。

这个函数虽然处理的是正整数，但它每次递归都调用 delete-units-digit，而不是把 n 每次减 1。而且它的终止条件也跟 n 有关，而不像前面的函数是一个常数。所以根据不同的目的，函数也有不同的变化，没有什么通用的模式可以用，但还是有规律可循，比如再写一个 count-digits 函数，数一数输入的数字是几位数。

下面给答案

(define count-digits
  (λ (n)
    (if (single-digit? n)
        1
        (+ 1 (count-digits
              (delete-units-digit n))))))

发现了吗，它跟 first-digit 函数很像，只有很小的改动。再之前的 expt 和 factorial 等函数也都很像。思考一下原因？

从它们的定义出发，如 expt 等函数就是要把自然数都数遍，所以采取每次减 1，但 count-digits 等函数不是从 1 到 n 一个数一个数算，而是 1 位数 1 位数的算，所以每次递归都是去掉个位数字。

最后练习题:
写出 sum-digits 函数，把每位数字加起来，比如

> (sum-digits 123)
6

建议:

(define get-units-digit ;; 取个位数字
  (λ (n)
    (remainder n 10))) ;; n/10 的余数

我们的 delete-units-digit 和 get-units-digit 配成了一对。刚好把一个数的个位和其它位数拆开。有了这两个函数，你可以对一个数的每位数字随意做文章。不信？作为思考题，你要不试试怎么把一个数翻转？(reverse-digits 123) => 321

这已经跟下一章的内容有所关联了。因为我们现在好像已经不是在玩一个数了，我们现在在把一个数当成一串数字玩。一个“数字列表”。

一道有点出戏的思考题:
如果 if 不是个特殊语法，而是个函数的话，比如我们重新定义

(define my-if
  (λ (pred conseq alt)
    (if pred conseq alt)))

然后用这个 my-if 重新定义前面的递归函数，会发生什么？

这也是为什么 if 只能是一个特殊语法，而不是一个函数。否则，递归就停不下来啦。

开个玩笑，你去谷歌一下“recursion”

最后作为一个练习，如果你还不太理解递归，就把前面的函数画画图吧。

当我学到递归的时候，我晚上做的梦都是递归的，我天天都意识到我在梦里做梦。现在只能祝你今天有个好梦了。

跳入梦中

再给出上一节中的 add-many-chips 和 factorial 函数。(上一节中的几个函数都是一样的道理)

(define add-many-chips
  (λ (num x)
    (if (= 0 num)
        x
        (add-chip (add-many-chips
                   (- num 1) x)))))

(define factorial
  (λ (n)
    (if (= 1 n)
        1
        (* n (factorial (- n 1))))))

下面是另一个 add-many-chips 的实现方式

(define add-many-chips
  (λ (num x)
    (if (= 0 num)
        x
        (add-many-chips (- num 1) ;; 这两行改变了
                        (add-chip x)))))

当然，先看懂它。

然后对比上一节中的图，我们画一下新版 (add-many-chips 3 666) 的图。(我就只画最终的情况了)

你可能发现了什么，我们的函数被串成一条直线了，也就是说，下面的 add-many-chips 函数返回了以后就没有别的事了。这个结果可以直接拿去输出。

这有什么区别呢？在现在很多流行语言里，没有区别，但是在 Racket 里，前面说过了，如果给一个很大的输入，旧的版本会占非常大的内存，但你试一下新的版本？它居然几乎不占内存。不管多大的输入都一样 (除了我电脑的风扇转得飞快，CPU 飙升到 60 多度…)

这就要提一个新的概念了，仔细看新版的那幅图，你会发现，因为下面的那个函数的返回值可以直接输出，所以当我们往下递归一次时，上面的函数就已经都没有用了。所以 Racket 很机智地就把这些函数都扔掉了，只留了下面那一个有用的。名副其实的功利主义者啊。

(注: 你用 DrRacket 的话，右下角可以看它的内存，你会发现内存一会儿上升一会儿又下降了，然后又慢慢上升…因为为了效率和简单性，Racket 不是一边计算一边扔没用的内存，而是过一段时间统一扔一次。这是一种计算机自动管理内存的方式，叫“垃圾回收(garbage collection)”，以后还会讲到。)

然后，由于这种递归是不会越来越占内存的，甚至比以前的递归方式效率还高，所以它专门有个名字，叫“尾递归(tail recursion)”。我现在不给详细的定义，但很显然，必须是要能把之前的东西全部扔掉的递归才能叫尾递归，对吧。(我这里其实撒了个谎，尾递归也有可能越来越占内存，比如参数引用了应该被扔掉的东西的时候，但这个以后再说吧，现在这么理解是没问题的)

下面做个挑战，把 factorial 函数改成尾递归模式。

你会发现这个有些难度。首先，因为是尾递归，所以当然要给它加一个参数。然后…然后我还是直接给答案吧，自己体会

(define factorial
  (λ (n)
    (fact-iter n 1)))
(define fact-iter ;; iterate，可以理解为循环
  (λ (n acc) ;; acc: accumulate 累积的结果
    (if (= 1 n)
        acc
        (fact-iter (- n 1)
                   (* n acc)))))
;; test
> (factorial 4)
=> (fact-iter 4 1)
=> (fact-iter 3 4)
=> (fact-iter 2 12)
=> (fact-iter 1 24)
24

这个真的讲不来，只能靠你自己体会了。

(以下内容考虑删掉，初学者请略过，直接跳到下一条分割线)

拓展内容:

其实这个函数跟原来的 factorial 不是完全对应的，它利用了乘法的什么什么律。原来是从1乘到n，现在是从n乘到1。要跟原来计算顺序对应，可以这么写

(define factorial
  (λ (n)
    (fact-iter n 1 1)))
(define fact-iter
  (λ (n counter acc)
    (if (= n counter)
        acc
        (fact-iter n
                   (+ 1 counter)
                   (* counter acc)))))

为什么要提这个呢？因为我们不用任何特殊的定律就可以转换，也就是说，我们有固定的方案转换这种递归!大致就是这样

(define f
  (λ (x)
    (if (= stop x)
        stop-value
        (g x (f (h x))))))
=>
(define f
  (λ (x)
    (f-iter x stop stop-value)))
(define f-iter
  (λ (x counter acc)
    (if (= x counter)
        acc
        (f-iter x (h' counter) (g (h' counter) acc)))))

其中 h' 是 h 的反函数，比如 h(x)=x-1，那么 h'(x)=x+1。g 可以是任意函数。

比如我们举个例子吧，取 h(x)=x-1，stop=0 简单理解一下

;; 非尾递归
> (f 3)
=> (g 3 (f 2))
=> (g 3 (g 2 (f 1)))
=> (g 3 (g 2 (g 1 (f 0))))
=> (g 3 (g 2 (g 1 stop-value)))

;; 尾递归
> (f 3)
=> (f-iter 3 0 stop-value)
=> (f-iter 3 1 (g 1 stop-value))
=> (f-iter 3 2 (g 2 (g 1 stop-value)))
=> (f-iter 3 3 (g 3 (g 2 (g 1 stop-value))))
=> (g 3 (g 2 (g 1 stop-value)))

考虑删掉的内容到此结束

练习题: 照着上面的 factorial 函数，把 expt 函数也转换成这种形式。

答案:

(define expt
  (λ (b n)
    (expt-iter b n 1)))
(define expt-iter
  (λ (b n acc)
    (if (= 0 n)
        acc
        (expt-iter b
                   (- n 1)
                   (* b acc)))))

下面的习题会告诉你自然数是怎么定义出来的。

首先，我们有一个 0，然后，我们有一个函数 add1，它能把一个数加 1。这是我们仅有的两个东西(当然，我们现在还不知道“两”是什么意思:)。

好了，接下来所有的自然数我们都有了，就像这样 (当然不要输到电脑里，因为数字不能做变量名，只是让你意会一下)

(define 1 (add1 0))
(define 2 (add1 1))
....
....

然后我们来定义加减乘除吧。

首先的难点就是，如何定义一个减 1 的函数 sub1

方法就是从 0 加上去，如果发现某个数加 1 以后等于参数，那么返回这个数

(define sub1
  (λ (x)
    (if (= 0 x)
        (error "sub1: invalid argument. expected: positive integer, given: 0")
        (sub1-iter x 0))))
(define sub1-iter
  (λ (x result)
    (if (= x (add1 result))
        result
        (sub1-iter x (add1 result)))))

然后定义加法

(define +
  (λ (a b)
    (if (= 0 a)
        b
        (add1 (+ (sub1 a) b)))))

;; 尾递归法
(define +
  (λ (a b)
    (if (= 0 a)
        b
        (+ (sub1 a) (add1 b)))))

练习题: 照同样的方式定义减法、乘法、除法，除法会略麻烦，因为有除不尽的情况，你可以选择直接向下取整。

下面两道练习题的口味有点重，看到数学就烦的人请略过。

练习题: 写出函数 prime?，判断一个数是否为质数 (方法: 从小到大找，如果找到一个因数((= 0 (remainder ? ?))) 就说明不是质数，如果一直找到足够大(自己思考是多大)都没找到，说明是质数)

练习题: 上一章中的倒数第二节的最后我们实现了一个开平方根的函数，现在修改它，让它最终精确到某个精确度而不是重复几次。用很小的小数和很大的数测试，确保都能得出适当的结果。因为计算机只能保存有限位小数，如果实现不恰当，有可能太大或太小的数就会陷入死循环。判断相邻两次递归结果不变时终止也不一定可行，因为可能最后几位小数一直来回摆动。总之自己去试吧。

这几题还是有点难度的，我不想给答案了，当时我都是自己写出来的，你们应该也有能力完成的。写出来以后记得稍微测试一下，但不要依赖于测试，在测试之前就要确保它是对的。(是不是听起来很矛盾)

好了，数学部分终于结束了

私有财产

回顾一下到现在为止函数的作用有哪些:
把一段程序的细节隐藏起来，提取重复的代码，和 define 结合起来可以递归。

是的，λ 还有跟 define 一样的作用，就是创造新的变量名字。

比如这样

> ((λ (x) (* x x))
   (+ 1 2))

这样也实现了 (+ 1 2) 的平方，应该没有疑问了吧。

它的用处在哪里呢？在函数里，或者 if 的分支中，即使你现在没想过，迟早你会想要定义一些临时的变量或函数的。一个很直接的想法就是，比如尾递归式的 factorial 等函数，不要让它们的 iter 函数暴露在外面。

其实 Racket 本身就提供了，不用辛苦地去套一层 λ 了。一个 λ 函数内可以先有一些 define 语句，最后跟着输出，比如

(define sum+sqr
  (λ (x y) ;; x+y 的平方
    (define a (+ x y))
    (* a a)))
;; 当然更推荐的是
(define sum+sqr
  (λ (x y)
    (sqr (+ x y))))

我们也可以改一下我们写过的那些函数。

(define factorial
  (λ (n)
    (define fact-iter
      (λ (n acc)
        (if (= 1 n)
            acc
            (fact-iter (- n 1)
                       (* n acc)))))
    (fact-iter n 1)))

这里，我们就是简单地把 fact-iter 的定义拿进来了，所以除了 factorial 这个函数，别的人就看不到它了。你需要先回忆一下上一章的内容，理解一下里面的 n 都是哪个 n，DrRacket 做得很好，你把鼠标移到变量上，它就会显示出这个变量来自哪里，还会把跟它相同的变量都加亮，跟它不同的不会变色。

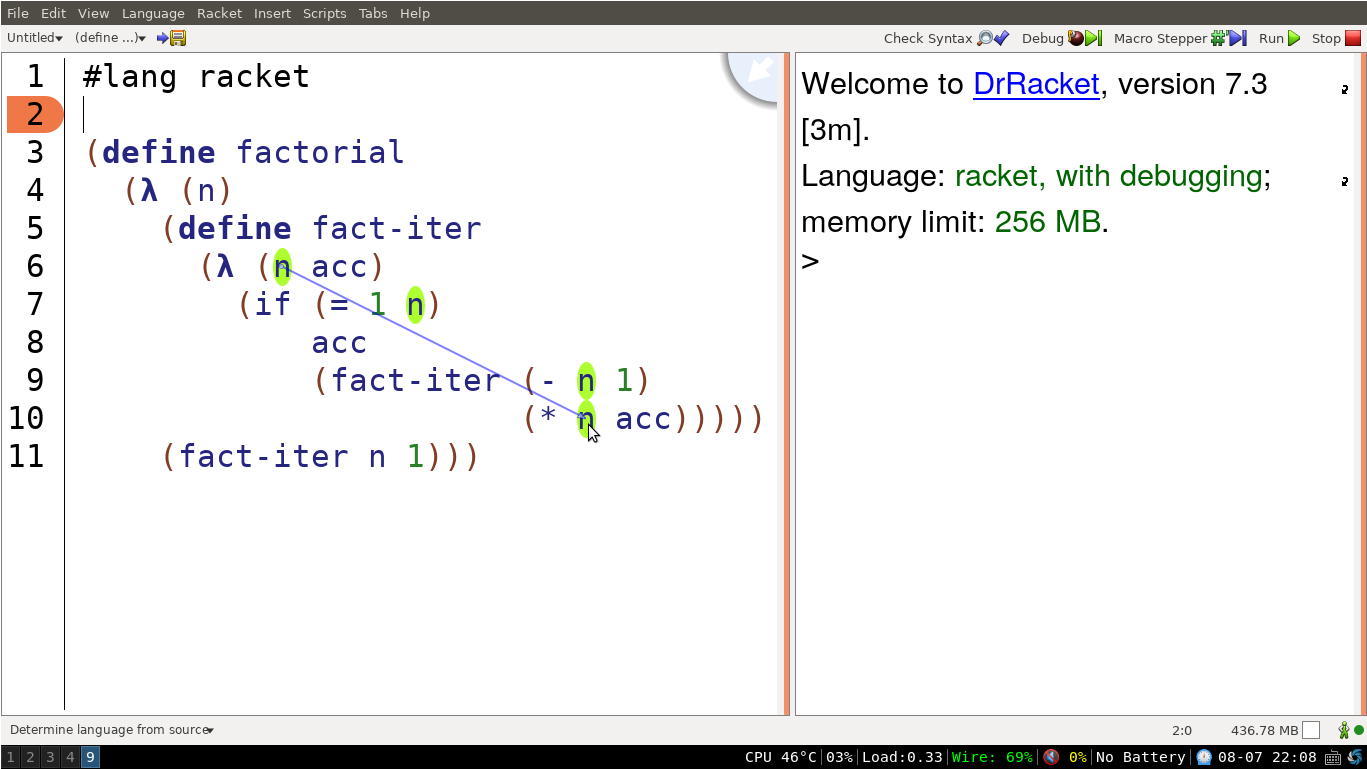
提醒一个常见的错误，可能有人想要定义一个函数，它能帮他定义很多东西，比如:

(define f
  (λ ()
    (define a 1)
    "define a"))
> (f)
"define a"
> a
; a: undefined;
;  cannot reference an identifier before its definition

虽然 a 是在 f 中定义的，但它的生命跟 f 的参数是一样短的，在 f 结束后就一起消失了(还不为它默哀？你们这些写出这段代码的人)。有想要这么干的人，请去网上搜“Racket 宏(macro)”，不保证你们能看懂。

也许你会觉得把一个函数挪进来没什么用，但反正作为一个好习惯，因为 fact-iter 也是 factorial 的实现细节，所以就不应该让别人看到，就先这么理解着吧。

对于一些函数来说，能够简化代码，比如

(define expt
  (λ (b n)
    (define expt-iter
      (λ (n acc)
        (if (= 0 n)
            acc
            (expt-iter (- n 1)
                       (* b acc)))))
    (expt-iter n 1)))

跟前面的 expt-iter 对比一下，你会发现我们可以省略一个参数 b，因为它一直是不变的，只是传来传去而已。

练习题: 同样的，把之前的 sqrt 函数用到的所有的函数都拿进来，尽可能地减少函数的参数。(原来的 f 有一个 a 一直传，现在可以消灭掉了)

注: 从这里开始一直到这章结尾的内容也考虑去掉

另外，因为接在 if 两个分支处要定义变量的情况非常普遍，有好几重 if 判断的情况也很普遍，Racket 还提供了一个语法叫 cond

(define abs
  (λ (x)
    (cond
      [(>= x 0) x]
      [else (- x)])))

(define prime?
  (λ (x)
    (define divisor?
      (λ (a b)
        (integer? (/ b a))))
    (define search
      (λ (n)
        (cond
          [(> n (sqrt x)) #t]
          [(divisor? n x) #f]
          [else (search (+ 1 n))])))
    (search 2)))

;; test
> (prime? 19260817)
#t
> (prime? 10000000)
#f
> (prime? 2)
#t
;; 我写完这种代码都不敢说一定是对的，一定要测试一下，
;; 不然写博客被打脸了怎么办

cond 的语法大致是这样

(cond
  [?1 v1]
  [?2 v2]
  [?3 v3]
  ....
  [else v-else])
;; ?n 和 vn 都可以是任意表达式

;; 若 ?1 则 v1，否则
;; 若 ?2 则 v2，否则
;; ....
;; 最终，如果上面都不满足，值为 v-else
;; else 这一行也可以省略，会默认变成一个报错语句:
;;      没有满足的条件

;; 也可以跟多个表达式
(cond
  [?1 def1 def2 .... defn v1]
  ....)
;; 其中 ?1 是判断条件，
;; def1 ~ defn 是 define 语句
;; v1 是最终的值

(注: 其实在 Racket 中，方括号和圆括号是不分的，只要它们能配对就行，但作为好习惯，这些函数调用和提供的语法都用圆括号，像 cond 中这些不表示一个“动作”的东西就用方括号，这样看起来会清楚得多)

这个语法可能有点麻烦。一般来说，语法都是有统一的格式的，记住一个以后，类似的就都记住了。

这就是所有的内容了，这章目前只是草稿，还有待修改和完善，另外如果有谁想出了更好的题目欢迎联系我。

PL教程 第二章 停下来!